题目描述

城市要新建​一个广场​，为了美观，要求​完全是正方形​。目前正在规划当中，正方形的大小和位置都在热烈的讨论之中。假设将可用于造广场的区域看成一个矩形，由 $1*1$ 的单位正方形构成。如下图：这是一个 $4*6$ 的矩形区域。

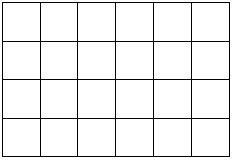
广场要求必须在这个矩形范围内，广场边线不能跨过任意一个单位正方形内部，只能与正方形边线重合，且广场必须为正方形。那么上图中，以下 $4$ 种正方形均为可行方案：

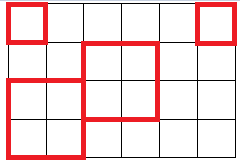
市民们提出了很多建造广场的方案。现在领导想要知道，到底有多少种不同的方案可以选择？请你设计一个程序，来计算以下建造广场的最多可行方案数。

输入格式

第一行两个整数 $n$ 和 $m$，表示用于建造广场区域的长和宽。

输出格式

一个整数，建造广场的可行方案数。

1 5

5

4 6

50

6 4

50

样例 $1$ 解释

$1*5$ 的矩形，只能构成 $1*1$ 的正方形。共有 $5$ 种不同的建造方法。

样例 $2$ 解释

$4*6$ 的矩形中，边长为 $1$ 的正方形有 $4*6$ 个，边长为 $2$ 的正方形有 $3*5$ 个，边长为 $3$ 的有 $2*4$ 个，边长为 $4$ 的的有 $1*3$ 个。共有 $24+15+8+3=50$ 个。

样例 $3$ 解释

和样例 $2$ 一样，只是行列不同。

数据范围

对于​ $40\%$ ​​的数据，$​n=1​$，​$1 \le m \le 100$；

对于 $70\%$ 的数据，$1 \le n \le m \le 100$；

对于 $100\%$ 的数据，$1 \le n,m \le 1000$。